L’un des principes fondamentaux de l’investissement est la notion d’intérêts. Que ce soit pour placer ton argent sur un compte épargne, investir en bourse ou souscrire à une assurance-vie, la manière dont les intérêts sont calculés peut avoir un impact significatif sur ton argent à long terme.
On distingue principalement deux types d’intérêts : les simples et les composés. Voyons ensemble leurs différences et leurs conséquences.
Comment fonctionnent les intérets simples ?
Les intérêts simples sont calculés uniquement sur l’argent investi. Autrement dit, les intérêts ne sont pas réinvestis dans le capital et le montant des intérêts que tu perçois reste identique chaque année.
Comment fonctionnent les intérets composés?
Les intérêts composés, en revanche, permettent de réinvestir les intérêts obtenus, ce qui génère un effet boule de neige car les intérêts augmentent de manière exponentielle avec le temps.
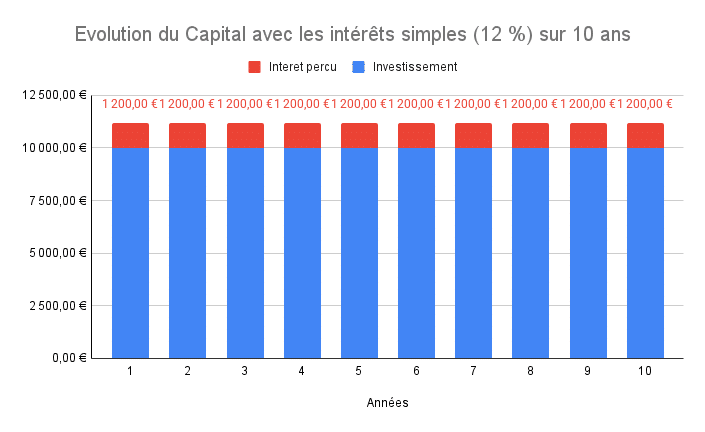
Cas pratique intérêts simples VS intérêts composés
Cas 1 : les intérêts simples (sans réinvestissement)
Dans ce premier cas, nous allons supposer que monsieur X souhaite retirer ses intérêts à la fin de chaque année. Nous avons les éléments suivants :
| Montant investi | Taux | Durée |
|---|---|---|
| 10 000 € | 12 % | 10 ans |
Notre premier cas s’enrichit de 1 200 € chaque année, on peut voir le graphique que le capital ne varie pas puisqu’il n’y a pas de réinvestissements des intérêts. Ce cas est typiquement le profil d’un rentier qui ne veut pas accroître son patrimoine financier et se contente uniquement de vivre de ses intérêts. Je te vois venir, oui, c’est impossible de vivre en France avec les sommes cités. Cependant imagine une minute si tu avais 1 million d’euros à placer cela ferait 120 000 € par an. De quoi passer une belle retraite et ceci sans travailler juste parce que tu as bien investi ton argent. Revenons à notre exemple, en résumé au bout de 10 ans nous avons gagné 12 000 € d’intérêts, mais si on les a dépensés, on est ni plus riche, ni plus pauvre qu’auparavant. Nous avons stagné financièrement.
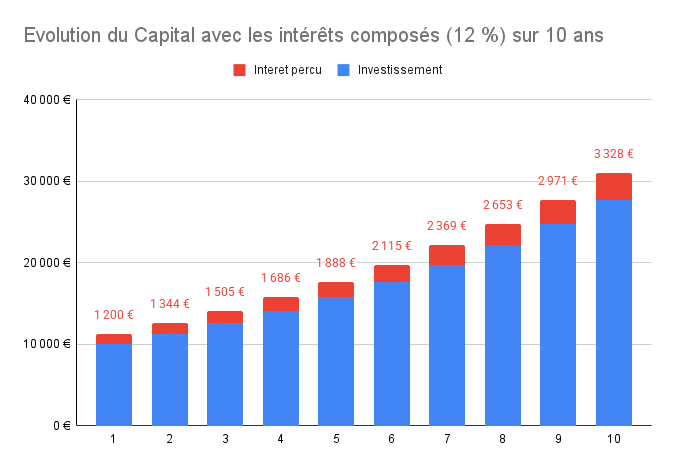
Cas 2 : les intérêts composés (avec réinvestissement)
Nous allons supposer que cette personne est un jeune actif et qu’il n’a pas besoin de son argent.
| Montant investi | Taux | Durée |
|---|---|---|
| 10 000 € | 12 % | 10 ans |

Comme cité plus haut les intérêts composés consistent à ne pas toucher aux intérêts que génère notre capital dans le but de réinvestir cet argent afin de le faire fructifier plus vite. Le graphique est très parlant puisqu’on voit bien que le capital augmente en même temps que les intérêts qui sont de plus en plus importants.
Cette méthode d’investissement est parfaitement adaptée à quelqu’un qui est dans la vie active et qui souhaite placer de l’argent et s’enrichir tout en maîtrisant le risque. Ici, on va chercher à faire des rendements moyens afin que notre patrimoine financier grossisse d’année en année.
Dans notre cas, le capital au bout de 10 ans s’élève à 31 058 € auxquels on retire 10 000 € d’investissement initial.
Pour résumer, on a investi 10 000 € et on a gagné 21 058 € d’intérêts.
Maintenant, je sais ce que tu vas me dire, : « moi, je veux profiter de mes intérêts pendant 10 ans et avoir un patrimoine équivalent à 31 058 €. » Tu veux le meilleur des deux mondes.
Cela tombe bien, c’est mon dernier exemple puisqu’il est possible d’avoir 31 058 €, mais cela n’est pas sans risques et ce cas est beaucoup plus compliqué à atteindre.
| Montant investi | Taux | Durée |
|---|---|---|
| 10 000 € | 12 % | 10 ans |
Cas 3 : je ne veux pas réinvestir mes intérêts, mais je souhaite atteindre un niveau d’intérêts équivalent à 21 058 € ?
Nous voulons déterminer le taux d’intérêts qui permettrait d’obtenir le même gain qu’avec le cas 2 soit 21 058 € d’intérêts.
Laisse-moi te dire que tout d’abord ce n’est pas forcément la meilleure solution de consommer son capital tout de suite. Dans la plupart des cas, il vaut mieux laisser son argent travailler tranquillement et une fois atteint un niveau qui nous convient, on le place pour qu’il puisse nous générer des intérêts et on vit sur ces intérêts. Cette méthode permet de vivre tranquillement sans jamais être à court d’argent.
| Montant investi | Taux | intérêts perçus pendant 10 ans | Capital dans 10 ans |
|---|---|---|---|
| 10 000 € | ? | 21 058 € | 31 058 € |
Nous voulons déterminer le taux d’intérêts qui permettrait d’obtenir le même gain qu’avec le cas 2 soit 21 058 € d’intérêts.
Je vous épargne une forte migraine en allant directement au résultat. on trouve 21,06 %.
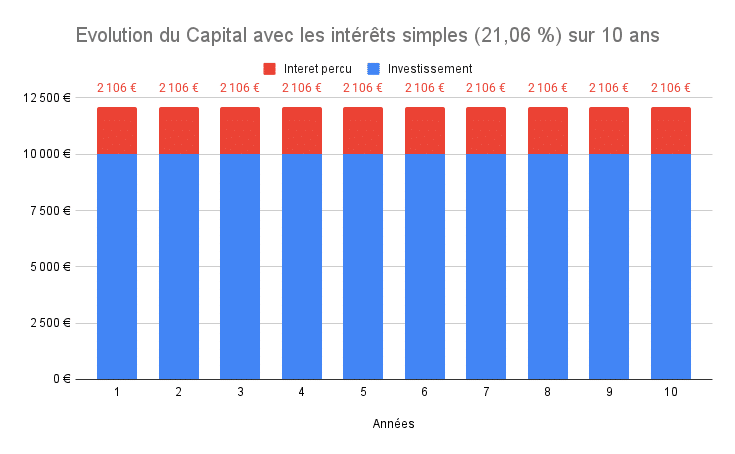
On voit qu’il faudrait quasiment doubler la rentabilité du placement pour avoir la même somme. Sans oublier le risque puisque pour avoir une rentabilité similaire, il faut prendre plus de risque et donc avoir une possibilité de se voir amputer une partie de son capital.
Comparaison des résultats
| Type d’intérêts | Capital final après 10 ans | Intérêts acquis | Taux nécessaire |
| Intérêts simples (Je retirer mes intérêts chaque année) | 10 000 € | 12 000 € | 12 % |
| Intérêts composés (Réinvestissement des intérêts) | 31 058 € | 21 058 € | 12 % |
| Intérêts simples (équivalent intérêts composés) | 31 058 € | 21 058 € | 21,06 % |
Comme on peut le voir, la différence est significative. Pour atteindre le même capital final il faudrait un taux d’intérêt beaucoup plus élevé (21,06 %).
Ce simple exemple illustre à quel point les intérêts composés peuvent faire augmenter un investissement de manière exponentielle. C’est pour cela qu’ils sont souvent considérés comme la « huitième merveille du monde », selon Albert Einstein.
Plus on commence tôt et plus la période d’investissement est longue, plus l’effet des intérêts composés est puissant.
Si tu souhaites faire croître ton capital de manière optimale, il est préférable de réinvestir tes gains et de laisser le temps jouer en ta faveur. L’effet boule de neige des intérêts composés est un levier puissant pour accumuler de la richesse à long terme.
Pour finir, voici une question qui illustre encore mieux l’importance des intérêts composés :
Tu préfères recevoir 3 millions € cash tout de suite ou bien recevoir 0,01 € qui double chaque jour pendant 30 jours ?
Prends un moment pour y réfléchir…
Si tu veux plus d’explication rien de mieux qu’une petite vidéo sur le sujet
Si tu veux en savoir plus….
Comment évaluer la performance de son portefeuille boursier ?
Comment évaluer la performance de son portefeuille boursier ? Investir en bourse est une démarche…
N’hésite pas à partager si cet article t’a aidé.
N’hésite pas à venir me rejoindre sur mes différents réseaux sociaux pour ne rien manquer.

